一、函数的概念
1、定义域:使表达式有意义的全体自变量的取值范围。
具体函数注意下列限制:
| $$\frac{f(x)}{g(x)},g(x)\neq0$$ | $$\sqrt[2n]{f(x)},f(x)\geq0$$ |
| $$\log_af(x)=\frac{\ln f(x)}{\ln a},f(x)>0$$ | $$cotf(x);cscf(x),f(x)\neq k\mathrm\pi$$ |
| $$\tan f(x);secf(x),f(x)=\frac{\mathrm\pi}2+k\mathrm\pi$$ | $$arc\sin f(x);arc\cos f(x),-1\leq f(x)\leq1$$ |
| $$g{(x)}^{f(x)}=e^{f(x)\ln g(x)},g(x)>0$$ |
2、值域:定义域中所有元素在某个对应法则下对应的所有的象所组成的集合,本质是求函数最大最小值。
3、反函数设函数y=f(x)的定义域是D,值域是f(D)。如果对于值域f(D)中的每一个y,在D中有且只有一个x使得g(y)=x,则按此对应法则得到了一个定义在f(D)上的函数,并把该函数称为函数y=f(x)的反函数,记为$$x=f^{-1}(y),y\in f(D)$$
二、函数的性质
1、单调性:若x1,x2∈D且x1<x2,有f(x1)<f(x2),称y=f(x)在区间内单调递增;若x1,x2∈D且x1<x2,有f(x1)>f(x2),称y=f(x)在区间内单调递减。
2、奇偶性:定义域关于原点对称,若f(0)有定义,则f(0)=0
f(-x)=f(x) 偶函数 图像关于y轴对称
f(-x)=-f(x) 奇函数 图像关于原点对称
3、周期性:f(x+T)=f(x),称f(x)为以T为周期的周期函数。(注:T一般指的是最小正周期,判断一个函数是否为周期函数用定义)
| 常见周期函数 | 周期 |
| $$sinx;cosx$$ | $$2\mathrm\pi$$ |
| $$sin(ax+b);cos(ax+b)$$ | $$\frac{2\mathrm\pi}{\left|\mathrm a\right|}$$ |
| $$tanx;cotx;\left|\sin x\right|;\left|\cos x\right|;cos^2 x;sin^2 x$$ | $$\mathrm\pi$$ |
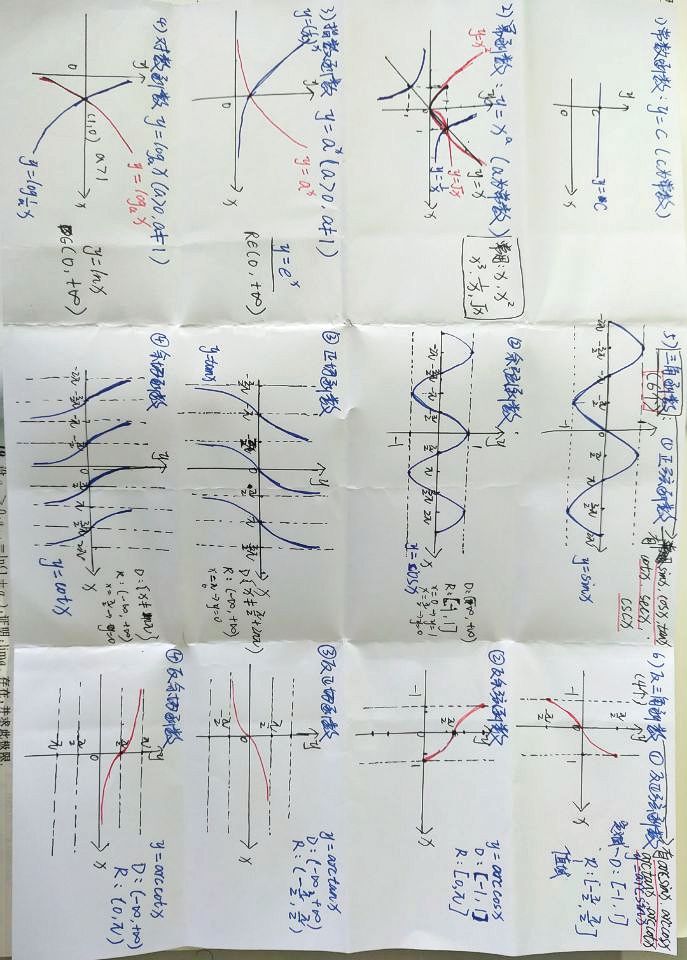
三、六类基本初等函数的图像(点击查看)
© 版权声明
文章版权归作者所有,未经允许请勿转载。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
THE END









暂无评论内容